Probability: Difference between revisions
(→Complex combinations/What are the odds of a specific number of things happening?: How many ways can I misspell Wolfram Alpha?) |
m (21 revisions imported) |
||
| (13 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
Are you into [[probability]] and [[statistics]]? | |||
* No? Start reading. | * No? Start reading. | ||
* Yes? Start editing. Know your audience, explain things for ordinary people. If I see any greek letters in here I'll bite off your kneecaps. | * Yes? Start editing. Know your audience, explain things for ordinary people. If I see any greek letters in here I'll bite off your kneecaps. | ||
| Line 11: | Line 11: | ||
In order to preserve the most information when writing anything, it's good practice to write your probabilities as (number of desired events)/(number of total possible events). The probability of rolling a 4, 5 or 6 is written as 3/6. | In order to preserve the most information when writing anything, it's good practice to write your probabilities as (number of desired events)/(number of total possible events). The probability of rolling a 4, 5 or 6 is written as 3/6. | ||
While 3/6 is numerically equivalent to 1/2, 50%, 0.5, or just .5, you do lose information regarding the total possible outcomes in simplifying fractions. However, it can be more informative to say 20% when saying "rolling a | While 3/6 is numerically equivalent to 1/2, 50%, 0.5, or just .5, you do lose information regarding the total possible outcomes in simplifying fractions. However, it can be more informative to say 20% when saying "rolling a 17+ on a d20," though. Unless you're in a probability class, the way you present your answer won't matter. | ||
The probability of an event E happening is written as | The probability of an event E happening is written as [[File:Probability Eq0.png|x30px]]. This is always a number between 0 and 1 (including 1 and 0). If you get something other than a number between 0 and 1, you're doing something wrong. | ||
===Inverse/What are the odds of something not happening?=== | ===Inverse/What are the odds of something not happening?=== | ||
| Line 19: | Line 19: | ||
===Compound/What are the odds of several things happening?=== | ===Compound/What are the odds of several things happening?=== | ||
The probability of any mutually exclusive events happening is the sum of the probabilities of each event. That is, since you cannot simultaneously roll a 1, 2, or 3 on a [[d6]], they are mutually exclusive events. The probability of rolling a 1, 2 or 3 on a [[d6]] is | The probability of any mutually exclusive events happening is the sum of the probabilities of each event. That is, since you cannot simultaneously roll a 1, 2, or 3 on a [[d6]], they are mutually exclusive events. The probability of rolling a 1, 2 or 3 on a [[d6]] is [[File:Probability Eq1.png|frameless|upright=1.25]]. | ||
For multiple events happening in a specific order over multiple trials, (for instance, the odds of rolling a d20 and getting four natural twenties in a row) take all the odds and multiply them together. So, the odds of rolling one natural twenty is 1/20. Two in a row? That's 1*1 / 20*20, or 1/400. Three in a row? 1/8000. Four? 1/160000. Getting a 9 on a d10 and then getting a 75 or higher on a d100 is 1/10*25/100 or 25/1000 or 1/40. | For multiple events happening in a specific order over multiple trials, (for instance, the odds of rolling a d20 and getting four natural twenties in a row) take all the odds and multiply them together. So, the odds of rolling one natural twenty is 1/20. Two in a row? That's 1*1 / 20*20, or 1/400. Three in a row? 1/8000. Four? 1/160000. Getting a 9 on a d10 and then getting a 75 or higher on a d100 is 1/10*25/100 or 25/1000 or 1/40. | ||
What does that mean for your chances of rolling a nat 20 if you just rolled one? Absolutely fucking nothing. Your dice don't remember what you just rolled, and if they did they wouldn't care. This is known as the Lack of Memory property, and is obvious from each event (roll) being independent. In notation, it would be | What does that mean for your chances of rolling a nat 20 if you just rolled one? Absolutely fucking nothing. Your dice don't remember what you just rolled, and if they did they wouldn't care. This is known as the Lack of Memory property, and is obvious from each event (roll) being independent. In notation, it would be [[File:Probability Eq2.png|frameless|upright=0.35]], or "the probability of rolling a 20, given that a 20 has already been rolled." | ||
Keep in mind that this is NOT the same as saying "rolling a d20 two times and getting at least one natural 20." The probability of this happening is actually 9.75%. Why? See below. | Keep in mind that this is NOT the same as saying "rolling a d20 two times and getting at least one natural 20." The probability of this happening is actually 9.75%. Why? See below. | ||
| Line 33: | Line 33: | ||
Calculating this rogue's chances is a matter of combining the rules we've looked at above. To get the expected number of hits we can just add the chances from each d20: <nowiki> P({rolling 9+ on a d20})=.6</nowiki>, so we would expect <nowiki> 2*.6=1.2 </nowiki> successes, and if we wanted expected damage we could stop there. | Calculating this rogue's chances is a matter of combining the rules we've looked at above. To get the expected number of hits we can just add the chances from each d20: <nowiki> P({rolling 9+ on a d20})=.6</nowiki>, so we would expect <nowiki> 2*.6=1.2 </nowiki> successes, and if we wanted expected damage we could stop there. | ||
However, this is clearly bullshit, because the rogue can't hit twice on one attack. To compensate for this, we subtract the chance of getting 9+ on ''both'' rolls. This gives us the real formula we want: | However, this is clearly bullshit, because the rogue can't hit twice on one attack. To compensate for this, we subtract the chance of getting 9+ on ''both'' rolls. This, known as the inclusion-exclusion principle, gives us the real formula we want: [[File:Probability Eq3.png|x30px]]. This rogue, then, is looking at a .6+.6-.36='''.84 chance to hit''', or only a 16% chance to miss that crucial backstab. | ||
We can get to this probability in a number of other ways, too. The simplest might be one minus the chance that neither attack hits. We know that's the product of the two miss rates, so this works out to | We can get to this probability in a number of other ways, too. The simplest might be one minus the chance that neither attack hits. We know that's the product of the two miss rates, so this works out to [[File:Probability Eq4.png|x30px]], or 1-(.4*.4)=.84. Convenient. | ||
To check, we could alternatively look at the three mutually exclusive ways we could succeed this attack. The rogue could A: hit on both dice, B: hit on the first but miss the second, or C: hit on the second but miss the first. For the numbers: | To check, we could alternatively look at the three mutually exclusive ways we could succeed this attack. The rogue could A: hit on both dice, B: hit on the first but miss the second, or C: hit on the second but miss the first. For the numbers: | ||
[[File:Probability Eq5.png|x60px]] | |||
We're now pretty sure we know the rogue's success rate, and are ready with the fleeing boots for that 16% failure chance. | |||
===Complex combinations/What are the odds of a specific number of things happening?=== | ===Complex combinations/What are the odds of a specific number of things happening?=== | ||
Having saved the rogue, we now go to 40k. We have a squad of ten tactical marines firing bolters into 3 plague zombies that we really need cleared off a victory point. For those that stumbled in here without knowing 40k (welcome to /tg!), each marine needs to roll several d6s to take out a zombie. First, they need 3+ on a d6 to hit, then 3+ on a d6 to wound, then the zombie needs to fail a 5+ Feel No Pain roll. What are the chances those tac marines will wipe out the zombies? Should we point a valuable squad of assault marines at them for support? | Having saved the rogue, we now go to 40k. We have a squad of ten tactical marines firing bolters into 3 plague zombies that we really need cleared off a victory point. For those that stumbled in here without knowing 40k (welcome to /tg/!), each marine needs to roll several d6s to take out a zombie. First, they need 3+ on a d6 to hit, then 3+ on a d6 to wound, then the zombie needs to fail a 5+ Feel No Pain roll. What are the chances those tac marines will wipe out the zombies? Should we point a valuable squad of assault marines at them for support? | ||
This is going to have an easy part and a hard one. The easy part is the chance of ''one'' marine killing ''one'' zombie. A d6 has a 4/6 chance of getting a 3+, and also a 4/6 chance of missing a 5+. This marine, then, has a 4/6 * 4/6 * 4/6 = 64/216 = 8/27 = '''29% chance''' to clip a zombie from the group. We've got ten marines, so our 'expected' number of dead zombies is 10*.29, or 2.9, just a little under the three we want. That suggests we should probably call up the assault marines, as there's a good chance we won't clear that whole group out. | This is going to have an easy part and a hard one. The easy part is the chance of ''one'' marine killing ''one'' zombie. A d6 has a 4/6 chance of getting a 3+, and also a 4/6 chance of missing a 5+. This marine, then, has a 4/6 * 4/6 * 4/6 = 64/216 = 8/27 = '''29% chance''' to clip a zombie from the group. We've got ten marines, so our 'expected' number of dead zombies is 10*.29, or 2.9, just a little under the three we want. That suggests we should probably call up the assault marines, as there's a good chance we won't clear that whole group out. | ||
| Line 49: | Line 53: | ||
We have ten marines and we're looking to put at least three unsaved wounds downrange, so we're looking for the number of ways to score precisely 3 successes in 10 tests. To make matters a little worse, we actually also need the number of ways to score 4 successes, or 5, or 6, or more, up to ten. Inflicting more wounds is not a problem for us. To work this out, we'll need the probability for a given scenario of hits, and the number of ways that scenario can occur. | We have ten marines and we're looking to put at least three unsaved wounds downrange, so we're looking for the number of ways to score precisely 3 successes in 10 tests. To make matters a little worse, we actually also need the number of ways to score 4 successes, or 5, or 6, or more, up to ten. Inflicting more wounds is not a problem for us. To work this out, we'll need the probability for a given scenario of hits, and the number of ways that scenario can occur. | ||
Let's look at inflicting exactly one wound. This requires one marine to succeed and all the others to fail. If we said that marine were the first guy in the squad we could tell how likely that is by multiplying everything together. We know the first marine succeeds and '''all''' the others fail, so this is | Let's look at inflicting exactly one wound. This requires one marine to succeed and all the others to fail. If we said that marine were the first guy in the squad we could tell how likely that is by multiplying everything together. We know the first marine succeeds and '''all''' the others fail, so this is [[File:Probability Eq6.png|x30px]] one success and nine fails, in that order. P(failure) is just 1-P(success), so we've got .29 and .71. | ||
The probability of any scenario like this, then, is just | The probability of any scenario like this, then, is just [[File:Probability Eq7.png|x30px]], or in this case, <nowiki>.29*.71*.71*.71*.71*.71*.71*.71*.71*.71 = .29*.71^9 = </nowiki> .29*.0458 = '''.0133'''. Wow, it sure got tedious in here. So, this 1.3% chance is the chance of scoring exactly one kill in exactly this way. | ||
We know there ten scenarios exactly like this one, differing only in which marine got the kill. We don't care about the difference, so those ten scenarios with 1.33% each give us 10*.0133 = .133, or a '''13.3% chance to kill exactly one zombie'''. | We know there ten scenarios exactly like this one, differing only in which marine got the kill. We don't care about the difference, so those ten scenarios with 1.33% each give us 10*.0133 = .133, or a '''13.3% chance to kill exactly one zombie'''. | ||
| Line 57: | Line 61: | ||
Now we can compute the possibility of any given scenario, but to inflict two wounds we would need to know how many ways you can organize two successes out of ten tests. Same thing for three, or four, or whatever else. For one success in ten tests, that was easy. For two or more, it's really annoying. Fortunately, we have this function on our calculators fittingly called a 'Combination': | Now we can compute the possibility of any given scenario, but to inflict two wounds we would need to know how many ways you can organize two successes out of ten tests. Same thing for three, or four, or whatever else. For one success in ten tests, that was easy. For two or more, it's really annoying. Fortunately, we have this function on our calculators fittingly called a 'Combination': | ||
Simply put, a Combination is the number of ways an event can occur in a set, ignoring order. This is important to us because we don't care what order these wounds are inflicted in and we don't want to spend all day multiplying numbers (only most of the day). A Combination combines two numbers, the number of | Simply put, a Combination is the number of ways an event can occur in a set, ignoring order. This is important to us because we don't care what order these wounds are inflicted in and we don't want to spend all day multiplying numbers (only most of the day). A Combination combines two numbers, the number of tests and the number of successes. | ||
I'm going to call the number of tests T and the number of successes S. The Combination of T and S is written 'T choose S', or TcS. | I'm going to call the number of tests T and the number of successes S. The Combination of T and S is written 'T choose S', or TcS. | ||
| Line 65: | Line 69: | ||
Know what a factorial is? In math, the exclamation point pulls double duty both as a point of excitement and also as notation for 'multiply this number by everything below it'. 5!, for example, is 5*4*3*2*1. Everyone learns about them in middle school, then nobody ever uses them. ...until now. | Know what a factorial is? In math, the exclamation point pulls double duty both as a point of excitement and also as notation for 'multiply this number by everything below it'. 5!, for example, is 5*4*3*2*1. Everyone learns about them in middle school, then nobody ever uses them. ...until now. | ||
[[File:Probability Eq7a.png|x90px]] | |||
So, 10C3 = 10! / (3! * 7!) = (10*9*8*7*6*5*4*3*2*1)/((3*2*1)*(7*6*5*4*3*2*1)). Cool thing is, the sequence 7*6*5*4*3*2*1 will always show up in the numerator and the denominator. We can cross it right off. | So, 10C3 = 10! / (3! * 7!) = (10*9*8*7*6*5*4*3*2*1)/((3*2*1)*(7*6*5*4*3*2*1)). Cool thing is, the sequence 7*6*5*4*3*2*1 will always show up in the numerator and the denominator. We can cross it right off. | ||
| Line 76: | Line 80: | ||
Alright, we've got our tool. Back on track. Ten marines, three zombies. The probability of any scenario that delivers '''S''' wounds from '''T''' marines with a per-marine kill rate of '''P''' is | Alright, we've got our tool. Back on track. Ten marines, three zombies. The probability of any scenario that delivers '''S''' wounds from '''T''' marines with a per-marine kill rate of '''P''' is [[File:Probability Eq8.png|x30px]]. There are '''TcS''' ways for that scenario to occur. We're down to the good stuff: | ||
Probability of inflicting exactly S wounds = | Probability of inflicting exactly S wounds = [[File:Probability Eq9.png|x30px]]. | ||
Exactly three wounds, ten marines, three zombies? 10c3 * (.29^3)*(.71^(10-3)). [https://www.wolframalpha.com/input/?i=combination(10,3)*(.29%5E3)*(.71%5E(10-3)) Wolfram Alpha, away!] '''26.6%''' | Exactly three wounds, ten marines, three zombies? 10c3 * (.29^3)*(.71^(10-3)). [https://www.wolframalpha.com/input/?i=combination(10,3)*(.29%5E3)*(.71%5E(10-3)) Wolfram Alpha, away!] '''26.6%''' | ||
| Line 84: | Line 88: | ||
Ever so close. That's the chance of exactly three unsaved wounds. We would be fine with four, or five, or any other number above three. So we need to either [https://www.wolframalpha.com/input/?i=sum+combination(10,j)*(.29%5Ej)*(.71%5E(10-j)),+j%3D3+to+10 add up everything above S=3], or [https://www.wolframalpha.com/input/?i=1-sum+combination(10,j)*(.29%5Ej)*(.71%5E(10-j)),+j%3D0+to+2 add the results for zero, one, and two wounds and subtract that from one]. '''59% chance.''' This game is going to be close, but the marines are more likely than not to win. | Ever so close. That's the chance of exactly three unsaved wounds. We would be fine with four, or five, or any other number above three. So we need to either [https://www.wolframalpha.com/input/?i=sum+combination(10,j)*(.29%5Ej)*(.71%5E(10-j)),+j%3D3+to+10 add up everything above S=3], or [https://www.wolframalpha.com/input/?i=1-sum+combination(10,j)*(.29%5Ej)*(.71%5E(10-j)),+j%3D0+to+2 add the results for zero, one, and two wounds and subtract that from one]. '''59% chance.''' This game is going to be close, but the marines are more likely than not to win. | ||
'''TL;DR''' The general form of all this is that if you have a number of tries T each with a success rate of P, the chance of getting exactly S successes is | '''TL;DR''' The general form of all this is that if you have a number of tries T each with a success rate of P, the chance of getting exactly S successes is [[File:Probability Eq9.png|x30px]]. If you're looking for at least S successes, add the results of this formula for everything between S and T. Or, if you're a real human with things to do, [https://www.wolframalpha.com/input/?i=sum+(combination(T,j)*(P%5Ej)*((1-P)%5E(T-j))),+j%3DS+to+T+where+P%3D.29,+S%3D3,+T%3D10 make a machine do it]. | ||
This is pretty easy to modify. Just change the inputs a little bit to try things out. [https://www.wolframalpha.com/input/?i=sum+(combination(T,j)*(P%5Ej)*((1-P)%5E(T-j))),+j%3DS+to+T+where+P%3D(2%2F3*2%2F3*2%2F3),+S%3D3,+T%3D20 Marines are rapid firing]? [https://www.wolframalpha.com/input/?i=sum+(combination(T,j)*(P%5Ej)*((1-P)%5E(T-j))),+j%3DS+to+T+where+P%3D(2%2F3*2%2F3),+S%3D3,+T%3D10 Plague zombies are normal cultists]? [https://www.wolframalpha.com/input/?i=sum+(combination(T,j)*(P%5Ej)*((1-P)%5E(T-j))),+j%3DS+to+T+where+P%3D(2%2F3*5%2F6*2%2F3),+S%3D4,+T%3D8 Eight devastators firing S8 AP3 krak missiles at a T6 3+ Carnifex with 5+ cover]? Enjoy. | This is pretty easy to modify. Just change the inputs a little bit to try things out. [https://www.wolframalpha.com/input/?i=sum+(combination(T,j)*(P%5Ej)*((1-P)%5E(T-j))),+j%3DS+to+T+where+P%3D(2%2F3*2%2F3*2%2F3),+S%3D3,+T%3D20 Marines are rapid firing]? [https://www.wolframalpha.com/input/?i=sum+(combination(T,j)*(P%5Ej)*((1-P)%5E(T-j))),+j%3DS+to+T+where+P%3D(2%2F3*2%2F3),+S%3D3,+T%3D10 Plague zombies are normal cultists]? [https://www.wolframalpha.com/input/?i=sum+(combination(T,j)*(P%5Ej)*((1-P)%5E(T-j))),+j%3DS+to+T+where+P%3D(2%2F3*5%2F6*2%2F3),+S%3D4,+T%3D8 Eight devastators firing S8 AP3 krak missiles at a T6 3+ Carnifex with 5+ cover]? Enjoy. | ||
| Line 109: | Line 113: | ||
d10 vs d12? That's 9+8+etc / 10*12, so 45/120. | d10 vs d12? That's 9+8+etc / 10*12, so 45/120. | ||
It turns out, if ''Y'' is larger than ''X'', the formula for the probability is very simple: | |||
[[File:Probability Eq10.png|x60px]] | |||
===What are the odds that adX beats bdY?=== | ===What are the odds that adX beats bdY?=== | ||
| Line 149: | Line 156: | ||
add up all the results and you have your answer!<br/> | add up all the results and you have your answer!<br/> | ||
====In general==== | |||
Now, I am a stats nerd with an undergrad education. I have spent several hours trying to figure out the exact probabilities for the sums of dice, which is probably more than any sane person would spend on this article. So I'm sure you don't care either. Plus, the math involves Greek letters, and I'm quite attached to my kneecaps. | |||
Fortunately, other stats nerds get tired of this shit too, so they discovered a good approximation: the normal distribution. This works well for 3dX and gets better the more dice you roll. | |||
Looking at my notes, for an adX the mean (average) is [[File:Probability Eq11.png|x50px]], and the "standard deviation" is [[File:Probability Eq12.png|x50px]]. That's all you need [https://www.wolframalpha.com/input/?i=normal+distribution+calculator&assumption=%7B%22F%22%2C+%22NormalProbabilities%22%2C+%22z%22%7D+-%3E%22-1%22&assumption=%7B%22F%22%2C+%22NormalProbabilities%22%2C+%22mu%22%7D+-%3E%220%22&assumption=%7B%22FVarOpt%22%7D+-%3E+%7B%7B%22NormalProbabilities%22%2C+%22sigma%22%7D%2C+%7B%22NormalProbabilities%22%2C+%22z%22%7D%2C+%7B%22NormalProbabilities%22%2C+%22mu%22%7D%7D to get an answer from Wolfram Alpha], but with a few caveats: You can't ask it for the probability that you'll roll ''exactly'' a number (it will pedantically tell you 0), but you can ask it the probability of rolling ''less than or equal'' or ''more than or equal'' to some number, and it doesn't respect the range of the dice pool (it will say it's possible, if unlikely, to roll a negative number, for example). | |||
So if, for whatever reason, you're doing a check roll for 12 or better on a 4d6, know that the mean is (4+4*6)/2 = 14 and the standard deviation is the square root of 182/3 (about 7.8), so the chance of passing the check is about [https://www.wolframalpha.com/input/?i=probability+that+x+%3E%3D+12+given+x+is+normally+distributed+mean%3D14+standard+deviation%3D7.8 60%]. | |||
==Statistics== | |||
If you're lazy or dealing with very weird rolls (What's the probability I'll get at least 4 successes on 10 dice, given that 1s remove a success but I ignore the first 1?) you can forgo the math and just roll the dice a million times and count the outcomes. Can't roll dice a million times? Computer can. Check out [http://topps.diku.dk/torbenm/troll.msp Troll Dice Roller]. It can take a bit of doing to figure out the formula, and some examples will require you to download and run the program locally, but it's fast and easy to understand the results. | |||
Latest revision as of 10:08, 22 June 2023
Are you into probability and statistics?
- No? Start reading.
- Yes? Start editing. Know your audience, explain things for ordinary people. If I see any greek letters in here I'll bite off your kneecaps.
The Basics[edit]
Relevant for: Everything
Notation/How do I write this stuff?[edit]
I'm assuming you know that a d4 is a four-sided-die, and 2d4 is two four-sided-dice. If you're confused regarding dice notation, see dice.
In order to preserve the most information when writing anything, it's good practice to write your probabilities as (number of desired events)/(number of total possible events). The probability of rolling a 4, 5 or 6 is written as 3/6.
While 3/6 is numerically equivalent to 1/2, 50%, 0.5, or just .5, you do lose information regarding the total possible outcomes in simplifying fractions. However, it can be more informative to say 20% when saying "rolling a 17+ on a d20," though. Unless you're in a probability class, the way you present your answer won't matter.
The probability of an event E happening is written as ![]() . This is always a number between 0 and 1 (including 1 and 0). If you get something other than a number between 0 and 1, you're doing something wrong.
. This is always a number between 0 and 1 (including 1 and 0). If you get something other than a number between 0 and 1, you're doing something wrong.
Inverse/What are the odds of something not happening?[edit]
If you're looking at a situation where something will either happen or not happen, then the odds of something not happening are equal to one minus the odds of it happening. So, the odds of rolling a 6 on a d6 is 1/6. The odds of not rolling one is 5/6. Add those together, you get 6/6, or 1. A lot of the time it's easier to work out the odds of something not happening and take the Inverse than to work out the odds of something happening.
Compound/What are the odds of several things happening?[edit]
The probability of any mutually exclusive events happening is the sum of the probabilities of each event. That is, since you cannot simultaneously roll a 1, 2, or 3 on a d6, they are mutually exclusive events. The probability of rolling a 1, 2 or 3 on a d6 is ![]() .
.
For multiple events happening in a specific order over multiple trials, (for instance, the odds of rolling a d20 and getting four natural twenties in a row) take all the odds and multiply them together. So, the odds of rolling one natural twenty is 1/20. Two in a row? That's 1*1 / 20*20, or 1/400. Three in a row? 1/8000. Four? 1/160000. Getting a 9 on a d10 and then getting a 75 or higher on a d100 is 1/10*25/100 or 25/1000 or 1/40.
What does that mean for your chances of rolling a nat 20 if you just rolled one? Absolutely fucking nothing. Your dice don't remember what you just rolled, and if they did they wouldn't care. This is known as the Lack of Memory property, and is obvious from each event (roll) being independent. In notation, it would be ![]() , or "the probability of rolling a 20, given that a 20 has already been rolled."
, or "the probability of rolling a 20, given that a 20 has already been rolled."
Keep in mind that this is NOT the same as saying "rolling a d20 two times and getting at least one natural 20." The probability of this happening is actually 9.75%. Why? See below.
Combination of Two/What are the odds of at least one thing happening in a set of two?[edit]
You're trying out DnD 5e, and you learn about its fancy new Advantage mechanic, where you can roll two d20s and take the higher of the two. If your rogue has advantage and needs a 9+ on a d20 to hit, what is the chance you're going to need to test out your new boots of frantically running away?
Calculating this rogue's chances is a matter of combining the rules we've looked at above. To get the expected number of hits we can just add the chances from each d20: P({rolling 9+ on a d20})=.6, so we would expect 2*.6=1.2 successes, and if we wanted expected damage we could stop there.
However, this is clearly bullshit, because the rogue can't hit twice on one attack. To compensate for this, we subtract the chance of getting 9+ on both rolls. This, known as the inclusion-exclusion principle, gives us the real formula we want: ![]() . This rogue, then, is looking at a .6+.6-.36=.84 chance to hit, or only a 16% chance to miss that crucial backstab.
. This rogue, then, is looking at a .6+.6-.36=.84 chance to hit, or only a 16% chance to miss that crucial backstab.
We can get to this probability in a number of other ways, too. The simplest might be one minus the chance that neither attack hits. We know that's the product of the two miss rates, so this works out to ![]() , or 1-(.4*.4)=.84. Convenient.
, or 1-(.4*.4)=.84. Convenient.
To check, we could alternatively look at the three mutually exclusive ways we could succeed this attack. The rogue could A: hit on both dice, B: hit on the first but miss the second, or C: hit on the second but miss the first. For the numbers:
We're now pretty sure we know the rogue's success rate, and are ready with the fleeing boots for that 16% failure chance.
Complex combinations/What are the odds of a specific number of things happening?[edit]
Having saved the rogue, we now go to 40k. We have a squad of ten tactical marines firing bolters into 3 plague zombies that we really need cleared off a victory point. For those that stumbled in here without knowing 40k (welcome to /tg/!), each marine needs to roll several d6s to take out a zombie. First, they need 3+ on a d6 to hit, then 3+ on a d6 to wound, then the zombie needs to fail a 5+ Feel No Pain roll. What are the chances those tac marines will wipe out the zombies? Should we point a valuable squad of assault marines at them for support?
This is going to have an easy part and a hard one. The easy part is the chance of one marine killing one zombie. A d6 has a 4/6 chance of getting a 3+, and also a 4/6 chance of missing a 5+. This marine, then, has a 4/6 * 4/6 * 4/6 = 64/216 = 8/27 = 29% chance to clip a zombie from the group. We've got ten marines, so our 'expected' number of dead zombies is 10*.29, or 2.9, just a little under the three we want. That suggests we should probably call up the assault marines, as there's a good chance we won't clear that whole group out.
Now, the tricky part. This is a really close game, and those assault marines are desperately needed elsewhere. We want the exact possibility the plague zombies won't survive. Open up Wolfram Alpha, and buckle up. Skip to the TL;DR if you just want a highly useful formula for mathhammering.
We have ten marines and we're looking to put at least three unsaved wounds downrange, so we're looking for the number of ways to score precisely 3 successes in 10 tests. To make matters a little worse, we actually also need the number of ways to score 4 successes, or 5, or 6, or more, up to ten. Inflicting more wounds is not a problem for us. To work this out, we'll need the probability for a given scenario of hits, and the number of ways that scenario can occur.
Let's look at inflicting exactly one wound. This requires one marine to succeed and all the others to fail. If we said that marine were the first guy in the squad we could tell how likely that is by multiplying everything together. We know the first marine succeeds and all the others fail, so this is ![]() one success and nine fails, in that order. P(failure) is just 1-P(success), so we've got .29 and .71.
one success and nine fails, in that order. P(failure) is just 1-P(success), so we've got .29 and .71.
The probability of any scenario like this, then, is just ![]() , or in this case, .29*.71*.71*.71*.71*.71*.71*.71*.71*.71 = .29*.71^9 = .29*.0458 = .0133. Wow, it sure got tedious in here. So, this 1.3% chance is the chance of scoring exactly one kill in exactly this way.
, or in this case, .29*.71*.71*.71*.71*.71*.71*.71*.71*.71 = .29*.71^9 = .29*.0458 = .0133. Wow, it sure got tedious in here. So, this 1.3% chance is the chance of scoring exactly one kill in exactly this way.
We know there ten scenarios exactly like this one, differing only in which marine got the kill. We don't care about the difference, so those ten scenarios with 1.33% each give us 10*.0133 = .133, or a 13.3% chance to kill exactly one zombie.
Now we can compute the possibility of any given scenario, but to inflict two wounds we would need to know how many ways you can organize two successes out of ten tests. Same thing for three, or four, or whatever else. For one success in ten tests, that was easy. For two or more, it's really annoying. Fortunately, we have this function on our calculators fittingly called a 'Combination':
Simply put, a Combination is the number of ways an event can occur in a set, ignoring order. This is important to us because we don't care what order these wounds are inflicted in and we don't want to spend all day multiplying numbers (only most of the day). A Combination combines two numbers, the number of tests and the number of successes.
I'm going to call the number of tests T and the number of successes S. The Combination of T and S is written 'T choose S', or TcS.
For the curious, the internal math on a Combination:
Know what a factorial is? In math, the exclamation point pulls double duty both as a point of excitement and also as notation for 'multiply this number by everything below it'. 5!, for example, is 5*4*3*2*1. Everyone learns about them in middle school, then nobody ever uses them. ...until now.
So, 10C3 = 10! / (3! * 7!) = (10*9*8*7*6*5*4*3*2*1)/((3*2*1)*(7*6*5*4*3*2*1)). Cool thing is, the sequence 7*6*5*4*3*2*1 will always show up in the numerator and the denominator. We can cross it right off.
10C3 = (10*9*8)/(3*2*1). Way better. Even by hand it's not too hard to get to 120. However, we didn't get to be the dominant species on the planet by doing things the hard way. Just make Wolfram Alpha do it: [1]
For the less curious, 10c3 = Make WolframAlpha do it: 120.
Alright, we've got our tool. Back on track. Ten marines, three zombies. The probability of any scenario that delivers S wounds from T marines with a per-marine kill rate of P is ![]() . There are TcS ways for that scenario to occur. We're down to the good stuff:
. There are TcS ways for that scenario to occur. We're down to the good stuff:
Probability of inflicting exactly S wounds = ![]() .
.
Exactly three wounds, ten marines, three zombies? 10c3 * (.29^3)*(.71^(10-3)). Wolfram Alpha, away! 26.6%
Ever so close. That's the chance of exactly three unsaved wounds. We would be fine with four, or five, or any other number above three. So we need to either add up everything above S=3, or add the results for zero, one, and two wounds and subtract that from one. 59% chance. This game is going to be close, but the marines are more likely than not to win.
TL;DR The general form of all this is that if you have a number of tries T each with a success rate of P, the chance of getting exactly S successes is ![]() . If you're looking for at least S successes, add the results of this formula for everything between S and T. Or, if you're a real human with things to do, make a machine do it.
. If you're looking for at least S successes, add the results of this formula for everything between S and T. Or, if you're a real human with things to do, make a machine do it.
This is pretty easy to modify. Just change the inputs a little bit to try things out. Marines are rapid firing? Plague zombies are normal cultists? Eight devastators firing S8 AP3 krak missiles at a T6 3+ Carnifex with 5+ cover? Enjoy.
Rolling for successes/hits[edit]
Relevant for: Shadowrun, old WoD, new WoD, others
What are the odds of me succeeding with X many dice?[edit]
You can work out the chances of every individual result, but the quickest way to figure out if you're going to get any successes at all is to take the Inverse of rolling no successes at all.
So, you've got 4d10 and you need an 8, 9 or 10 to succeed? You've got a .3 chance of a success on one die, meaning you have a .7 chance a failure on one. You're rolling four dice, so the odds of all of them being failures is .7^4, or 0.7*0.7*0.7*0.7, or 0.2401. The inverse of that, the odds of getting anything other than zero successes, is 0.7599.
Incidentally, if you're working with that Target Number 8 in the last paragraph and you want a quick way to work out your chance of success... The odds of failing outright with two dice are 0.49, or about 1/2. That means the odds of failing with four dice are about 1/4. Six dice gives you 1/8, eight gets you 1/16, or 15/16 chance of getting at least one success. Repeat as many times as you like.
There are tables floating around, but I cannot into embedding images. http://wiki.white-wolf.com/exalted/index.php?title=Dice_Probability/Heroic,_TN_7
General Polyhedral Dice[edit]
Relevant for: Dungeons and Dragons
What are the odds that dX beats dY?[edit]
Want to know if a d6 is going to beat a d12? First, there are 72 ways this could come out (6 times 12, from the two dice), so the answer will be X/72. Next, look at it this way:
If the d12 lands on a 6 or higher, then the d6 will not be higher than it. If it lands on a 5, then one of the results on the d6, the 6, would be higher than it. So that's 1/72 so far. If it lands on a 4 then there are two results, if it lands on a 1 then there are five. There's a total of 1+2+3+4+5 results that would make the d6 the higher die, 15 in total. The odds of a d6 being higher than a d12 are 15/72.
d10 vs d12? That's 9+8+etc / 10*12, so 45/120.
It turns out, if Y is larger than X, the formula for the probability is very simple:

What are the odds that adX beats bdY?[edit]
step 1: AdX (sum the results) yields a number between A (when you roll all ones) and A*X (when you roll all X's (i.e. 6's). The trick here is that there are more results than sums, and so you need to work out how often these sums occur for your results.
lets look at 2d6 : there are 36 unique unique combinations of 1 through 6 (taken twice)
2 can occur 1 way (1/36)
3 can occur 2 ways (2/36)
4 can occur 3 ways (3/36)
5 can occur 4 ways (4/36)
6 can occur 5 ways (5/36)
7 can occur 6 ways (6/36)
8 can occur 5 ways (5/36)
9 can occur 4 ways (4/36)
10 can occur 3 ways (3/36)
11 can occur 2 ways (2/36)
12 can occur 1 way (1/36)
lets look at the corresponding 2d10: there are 100 unique combinations of 1 through 10 (taken twice) these can sum up to
2 can occur 1 way (1/100)
3 can occur 2 ways (2/100)
4 can occur 3 ways (3/100)
5 can occur 4 ways (4/100)
6 can occur 5 ways (5/100)
7 can occur 6 ways (6/100)
8 can occur 7 ways (7/100)
9 can occur 8 ways (8/100)
10 can occur 9 ways (9/100)
11 can occur 8 ways (8/100)
12 can occur 7 ways (7/100)
13-20 can occur 36 ways (36/100)
So for 2d6 to beat 2d10:
one way is 2d6 =3 and 2d10 = 2 (2/36)*(1/100)
one way is 2d6 =4 and 2d10 = 2 (3/36)*(1/100) or one way is 2d6 =4 and 2d10 = 3 (3/36)*(2/100)
one way is 2d6 =5 and 2d10 = 2 (4/36)*(1/100) or one way is 2d6 =5 and 2d10 = 3 (4/36)*(2/100)or one way is 2d6 =5 and 2d10 = 4 (4/36)*(3/100)
add up all the results and you have your answer!
In general[edit]
Now, I am a stats nerd with an undergrad education. I have spent several hours trying to figure out the exact probabilities for the sums of dice, which is probably more than any sane person would spend on this article. So I'm sure you don't care either. Plus, the math involves Greek letters, and I'm quite attached to my kneecaps.
Fortunately, other stats nerds get tired of this shit too, so they discovered a good approximation: the normal distribution. This works well for 3dX and gets better the more dice you roll.
Looking at my notes, for an adX the mean (average) is 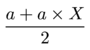 , and the "standard deviation" is
, and the "standard deviation" is  . That's all you need to get an answer from Wolfram Alpha, but with a few caveats: You can't ask it for the probability that you'll roll exactly a number (it will pedantically tell you 0), but you can ask it the probability of rolling less than or equal or more than or equal to some number, and it doesn't respect the range of the dice pool (it will say it's possible, if unlikely, to roll a negative number, for example).
. That's all you need to get an answer from Wolfram Alpha, but with a few caveats: You can't ask it for the probability that you'll roll exactly a number (it will pedantically tell you 0), but you can ask it the probability of rolling less than or equal or more than or equal to some number, and it doesn't respect the range of the dice pool (it will say it's possible, if unlikely, to roll a negative number, for example).
So if, for whatever reason, you're doing a check roll for 12 or better on a 4d6, know that the mean is (4+4*6)/2 = 14 and the standard deviation is the square root of 182/3 (about 7.8), so the chance of passing the check is about 60%.
Statistics[edit]
If you're lazy or dealing with very weird rolls (What's the probability I'll get at least 4 successes on 10 dice, given that 1s remove a success but I ignore the first 1?) you can forgo the math and just roll the dice a million times and count the outcomes. Can't roll dice a million times? Computer can. Check out Troll Dice Roller. It can take a bit of doing to figure out the formula, and some examples will require you to download and run the program locally, but it's fast and easy to understand the results.

